Quantum states generally represent the possible conditions of a quantum system in terms of a mathematical entity. For example- the spin of an electron can be either up or down so there are two quantum states and this can further be represented as a superposition using Bra-Ket or Dirac notation.
In principle, quantum states are categorized into two types: pure states and mixed states. A pure state is principally the natural state of a quantum system and carries with it the exact information of the overall system. On the other hand, a mixed state has limited information about a particular quantum system and is usually an ensemble of probabilities. Talking of their representation, pure states are denoted by a ray in a Hilbert space over complex numbers whereas mixed states are represented by density matrices.
Inspired by the infamous Schrodinger’s cat gedankenexperiment, physicists have determined a special quantum state and have termed them as cat states. A unique feature of cat states is that they can be written down as superpositions of two states with opposite phases. In other words, they are states that can be represented as a linear combination of two completely opposite situations, for example – dead and alive as in Schrodinger’s cat scenario.
It is well understood that classical computers are foundationally based on bits that exchange information using the binary digits 0 or 1. However, quantum computers are built from qubits that are technically in a superposed state. Although quantum computers are more significant than standard computers in multiple respects, they are at a higher risk of errors since there are additional sources of error in a quantum computer which mainly emerge from employing the qubits.
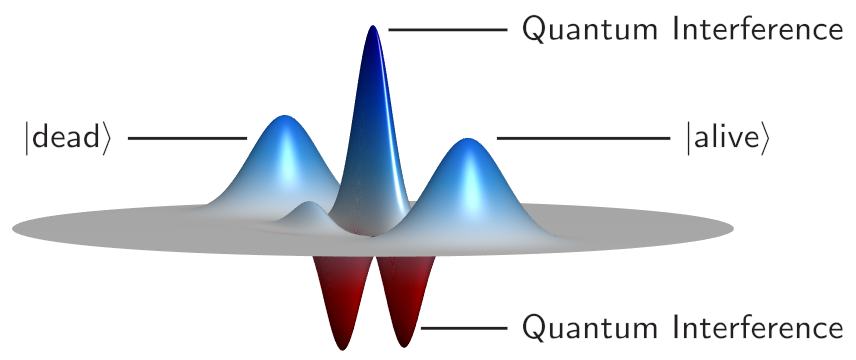
Wigner function for a Schrödinger cat state. The bell shapes represent the “alive” and “dead” possible states for the “cat” and the oscillations between them indicate the quantum coherence between these states (i.e., the classic “both alive and dead” statement). A similar Wigner function without these interference terms would represent a state with a classical coin toss probability of being either alive or dead but not both. The presence of the interference terms indicates that this Wigner function represents a state that is in both states (“alive and dead”) at the same time (a superposition). Figure and description source: Physical Review A
Now, a recent work by researchers at the RIKEN Center for Quantum Computing shows that using cat states could help achieve fault tolerance in quantum computing [1]. It is expected that when a quantum computer is built from qubits that operate on cat states, one could achieve fault-tolerant quantum gates for connecting the qubits in a network that is essentially non-local.
Fault tolerance can be defined as the ability of a system to continue its operation under a circumstance wherein an error leads to a fault in one or more of its components. The practical applications of this property are multifold and it has led to the emergence of numerous sub-research fields within quantum physics such as quantum error correction, quantum algorithms, and quantum supremacy among others.
The applications of fault-tolerant quantum computation are quite diverse in that it would allow making computations that were previously not feasible through standard techniques. It would also allow searching databases in a way that is more efficient than standard computers and this would be possible by the execution of quantum search algorithms.
Ye-Hong Chen, who is the corresponding author of the study, explains: “Let us assume that you are searching for one key that will open a box among 100 keys. On average, you would need to try 50 keys using a conventional search algorithm to identify the one key that opens that box. But with the quantum search algorithm the average is only 10 attempts.”
References
[1] Ye-Hong Chen et al, Fault-Tolerant Multiqubit Geometric Entangling Gates Using Photonic Cat-State Qubits, Phys. Rev. App. (2022). DOI: 10.1103/PhysRevApplied.18.024076